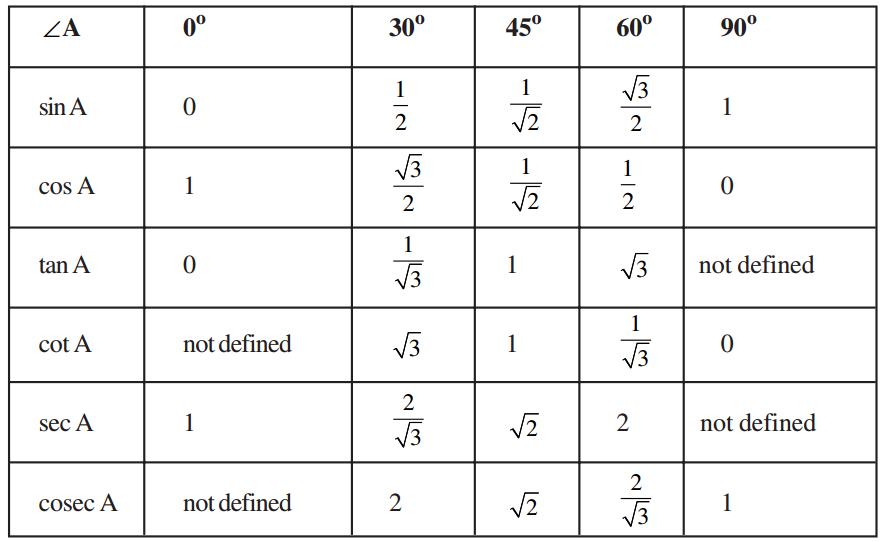
Sin Cos Tan
Sin, Cos, & Tan Ratios Find the value of each trigonometric ratio. Write each as a FRACTION and a DECIMAL. 1) sin A 18 24 A 30 B C 2) sin C 32 24 40 C B A 3) sin C 24 7 25 C B A 4) sin C 24 18 30 C A 5) sin X 28 21 35 X Y Z 6) sin Z 16 30 34 Z Y X 7) sin X 20 15 25 X Y Z 8) sin A 15 8 17 A B C 9) sin A 14 48 A 50 B C 10) sin Z 30 40 50 Z Y X-1. Feb 23, 2021 Trig calculator finding sin, cos, tan, cot, sec, csc To find the trigonometric functions of an angle, enter the chosen angle in degrees or radians. Underneath the calculator, six most popular trig functions will appear - three basic ones: sine, cosine and tangent, and their reciprocals: cosecant, secant and cotangent.
by M. Bourne
For the angle θ in a right-angled triangle as shown, we name the sides as:
- hypotenuse (the side opposite the right angle)
- adjacent (the side 'next to' θ)
- opposite (the side furthest from the angle θ)
We define the three trigonometrical ratios sine θ, cosine θ, and tangent θ as follows (we normally write these in the shortened forms sin θ, cos θ, and tan θ):
`sin theta=text(opposite)/text(hypotenuse)` `cos theta =text(adjacent)/text(hypotenuse)``tan theta =text(opposite)/text(adjacent)`
To remember these, many people use SOH CAH TOA, that is:
Sin θ = Opposite/Hypotenuse,
Cos θ = Adjacent/Hypotenuse, and
Tan θ = Opposite/Adjacent
The Reciprocal Trigonometric Ratios
Often it is useful to use the reciprocal ratios, depending on the problem. (In plain English, the reciprocal of a fraction is found by turning the fraction upside down.)
`'cosecant' θ` is the reciprocal of `'sine' θ`,
`'secant' θ` is the reciprocal of `'cosine' θ`, and
`'cotangent' θ` is the reciprocal of `'tangent' θ`
We usually write these in short form as `csc θ`, `sec θ` and `cot θ`. (In some textbooks, 'csc' is written as 'cosec'. It's the same thing.)
`csc theta =text(hypotenuse)/text(opposite)` `sec theta =text(hypotenuse)/text(adjacent)` `cot theta =text(adjacent)/text(opposite)`
Important note: There is a big difference between csc θ and sin-1 θ.
- The first one is a reciprocal: `csc theta=1/(sin theta)`.
- The second one involves finding an angle whose sine is θ.
So on your calculator, don't use your sin-1 button to find csc θ.
We will meet the idea of sin-1θ in the next section, Values of Trigonometric Functions.
The Trigonometric Functions on the x-y Plane
For an angle in standard position, we define the trigonometric ratios in terms of x, y and r:
`sin theta =y/r` `cos theta =x/r``tan theta =y/x`
Notice that we are still defining
sin θ as `'opp'/'hyp'`;
cos θ as `'adj'/'hyp'`, and
tan θ as `'opp'/'adj'`,
but we are using the specific x-, y- and r-values defined by the point (x, y) that the terminal side passes through. We can choose any point on that line, of course, to define our ratios.
To find r, we use Pythagoras' Theorem, since we have a right angled triangle:
`r=sqrt(x^2+y^2)`

Not surprisingly, the reciprocal ratios are defined similarly in terms of the x-, y- and r-values as follows:
`csc theta =r/y` `sec theta =r/x``cot theta =x/y`
We will see some examples of finding exact values in the next section, Values of Trigonometric Functions ».
by M. Bourne
For the angle θ in a right-angled triangle as shown, we name the sides as:
- hypotenuse (the side opposite the right angle)
- adjacent (the side 'next to' θ)
- opposite (the side furthest from the angle θ)
We define the three trigonometrical ratios sine θ, cosine θ, and tangent θ as follows (we normally write these in the shortened forms sin θ, cos θ, and tan θ):
`sin theta=text(opposite)/text(hypotenuse)` `cos theta =text(adjacent)/text(hypotenuse)``tan theta =text(opposite)/text(adjacent)`
To remember these, many people use SOH CAH TOA, that is:
Sin θ = Opposite/Hypotenuse,
Cos θ = Adjacent/Hypotenuse, and
Tan θ = Opposite/Adjacent
The Reciprocal Trigonometric Ratios
Often it is useful to use the reciprocal ratios, depending on the problem. (In plain English, the reciprocal of a fraction is found by turning the fraction upside down.)
`'cosecant' θ` is the reciprocal of `'sine' θ`,
`'secant' θ` is the reciprocal of `'cosine' θ`, and
`'cotangent' θ` is the reciprocal of `'tangent' θ`
We usually write these in short form as `csc θ`, `sec θ` and `cot θ`. (In some textbooks, 'csc' is written as 'cosec'. It's the same thing.)
`csc theta =text(hypotenuse)/text(opposite)` `sec theta =text(hypotenuse)/text(adjacent)` `cot theta =text(adjacent)/text(opposite)`
Important note: There is a big difference between csc θ and sin-1 θ.
- The first one is a reciprocal: `csc theta=1/(sin theta)`.
- The second one involves finding an angle whose sine is θ.
So on your calculator, don't use your sin-1 button to find csc θ.
We will meet the idea of sin-1θ in the next section, Values of Trigonometric Functions.
The Trigonometric Functions on the x-y Plane
For an angle in standard position, we define the trigonometric ratios in terms of x, y and r:
`sin theta =y/r` `cos theta =x/r``tan theta =y/x`
Sin Cos Tan Circle
Notice that we are still defining
sin θ as `'opp'/'hyp'`;
cos θ as `'adj'/'hyp'`, and
tan θ as `'opp'/'adj'`,
but we are using the specific x-, y- and r-values defined by the point (x, y) that the terminal side passes through. We can choose any point on that line, of course, to define our ratios.
To find r, we use Pythagoras' Theorem, since we have a right angled triangle:
`r=sqrt(x^2+y^2)`
Not surprisingly, the reciprocal ratios are defined similarly in terms of the x-, y- and r-values as follows:
`csc theta =r/y` `sec theta =r/x``cot theta =x/y`
Sin Cos Tan Csc Sec Cot
We will see some examples of finding exact values in the next section, Values of Trigonometric Functions ».